Fractura concoidea

Concoide

La fractura concoidea o concoidal es un tipo de rotura con forma de concha,​ que presenta una cara cóncava en un fragmento y convexa en el complementario y la superficie puede ser lisa o con estrías concéntricas.​ Es propia de materiales frágiles, de composición homogénea, pero amorfa (isótropa), que al trocearse no siguen planos naturales de separación. Entre estos materiales podemos incluir el vidrio doméstico, algunos minerales (cristal de roca) y numerosas rocas naturales duras y criptocristalinas como el sílex, la cuarcita, la obsidiana, el jaspe, etc.

La fractura concoidea se opone a la fractura plana, o, más propiamente, exfoliación, que tienen ciertos cuerpos cristalinos en los que las moléculas están ordenadas en una única dirección, por ejemplo las gemas o los materiales semiconductores. Cada uno de estos tipos de fractura tiene propiedades aprovechables por el ser humano. Así, la fractura concoidea es empleada por muchos geólogos para determinar la naturaleza de los materiales que estudian, pero su verdadera importancia radica en que fue el sistema con el que se fabricaron todas las herramientas talladas en piedra de la Prehistoria.

Véase también: Talla lítica

Descripción

Fractura concoidea del jaspe rojo. Puede verse en el centro de la imagen, la típica forma de concha en este tipo de fractura

cono neutro de fractura

Cara inferior de una lasca experimental de obsidiana donde se aprecian las alteraciones reológicas de la fractura concoidea

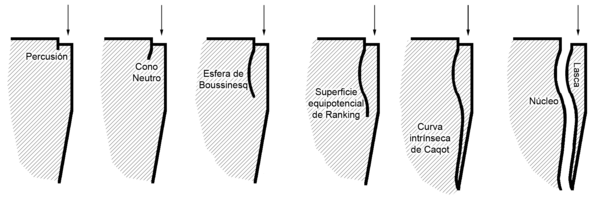
La fractura concoidea se produce a través de una superficie equipotencial que no es plana, una onda curva que además cambia paulatinamente a medida que se propaga. El nacimiento es la parte donde el material recibe la tensión que va a provocar la fractura (bien por impacto o por una fuerte presión). Esta zona recibe el nombre de superficie elíptica de Hertz,​ y a partir de ella, como si de un epicentro se tratase, se desarrollan ondas de vibración que rompen el material. En realidad, se trata de ondas elásticas transversales que son reflejadas una y otra vez por todas las caras del sólido hasta que, por fin, confluyen en una única superficie de fractura. Estas ondas tienen forma de parábolas anchas y cortas cuyo origen es tangente (parábolas homofocales). A continuación, se desarrolla un cono hertziano o cono neutro que va curvándose hasta convertirse en la esfera de Boussinesq (básicamente, el concoide).​ A medida que la superficie de fractura se propaga, las parábolas cambian de dirección a través de la llamada superficie equipotencial de Ranking), así, la onda se va deformando, hasta formar la curva intrínseca de Caqot.

La fractura concoidea perfecta es a menudo llamada hookiana​ y adquiriría una forma elíptica ancha y corta, ya que la parábola homofocal es la morfología propia de las ondas de fractura en condiciones ideales. Esta forma recuerda a la concha de un bivalvo, razón por la cual recibe el nombre de concoidea. La morfología elíptica no es intrínsecamente mejor o peor, pero para los humanos de la Prehistoria suponía unas claras limitaciones, ya que sólo podría proporcionar piezas anchas y cortas: lascas.

Sin embargo hay muchos elementos que alteran la propagación de las ondas por lo que es normal que estas degeneren adquiriendo propiedades llamadas reológicas. Por ejemplo, las propias ondas elásticas que siguen rebotando y que interfieren el normal desarrollo de la fractura; también las fisuras o las impurezas del material. Todos esos factores perturban la fractura natural, desorganizándola, generando superficies de rotura secundarias, astillamientos caóticos; lancetas radiales que indican de dónde viene el impacto y cuál es el desarrollo de la superficie de fractura; esquirlas parásitas que saltan fortuitamente, pero de un modo sistemático en el concoide; microlascados trapezoidales, asociados a los bordes de la lasca, donde el material es más fino y vulnerable a la repercusión de interferencias; ondulaciones que provocan un movimiento oscilatorio en la superficie de fractura como las olas del agua, etc. Uno de los mecanismos más interesantes es el llamado efecto borde.

Aprovechamiento humano

Existe cierta relación entre el espesor del sólido y la superficie de fractura, ya que sus paredes exteriores reflejan continuamente las ondas elásticas transversales. Cuando las ondas de fractura se acercan a la superficie del cuerpo, cambian bruscamente su dirección, propagándose hacia dicha superficie, a eso le llamamos efecto borde. Si hablamos de artefactos líticos tallados en rocas de fractura concoidea, el efecto borde, lejos de ser un inconveniente para los artesanos prehistóricos fue aprovechado para obtener piezas con formas y dimensiones previstas, consiguiendo, así, una serie de productos, de forma preconcebida por el artesano tallista, que reciben el nombre genérico de lascas, pero que pueden dividirse en muchas variedades verdaderamente significativas para los arqueólogos. Caso especial es el de las hojas líticas; ya que la fractura concoidea natural tiende a ser más ancha que larga y, sin embargo, gracias al dominio del efecto borde, los artesanos prehistóricos conseguían productos extremadamente alargados y finos, muy adecuados para numerosos utensilios.

Una hoja lítica

Véanse también: Lasca y Hoja lítica.

Bibliografía

• Bertouille, Horace (1989). Théories physiques et mathématiques de la taille de outils préhistoriques. Cahiers du Quaternaire, nº 15, Editions du CNRS. ISBN 2-222-04377-8. 
• Benito del Rey, Luis y Benito Álvarez, José-Manuel (1999). Métodos y materias instrumentales en Prehistoria y Arqueología. Tomo II.-Tecnología y tipología. Gráficas Cervantes, S.A. (Salamanca). ISBN 84-95195-05-4 (páginas 38-42). 
• Dauvois, Michel (1976). «Fracture ou éclatement par percussion et par pression. Stigmates. schéma diacritique». Precis de dessin dynamique et structural des industries lithiques préhistoriques. CNRS - Pierre Fanlac (París). (páginas 165-201). 

• Datos: Q2747476
• Multimedia: Conchoidal fracture / Q2747476